[最も選択された] モーメント 数学 454047-モーメント 意味 数学
モーメント (数学) 画像のモーメント 2変数関数 f(x, y) の (m n) 次モーメント μ m n ( 0 ) {\displaystyle \mu _{mn}^{(0)}} は、 μ モーメント (数学) 画像のモーメントモーメント_(数学)を解説文に含む見出し語の英和和英辞典の検索結果です。モーメント (数学)数学の確率論および関係した諸分野におけるモーメント (moment) または積率(せきりつ)とは、物理学におけるモーメントを抽象化した概念である。数学的準備 2次式 平方完成,2次方程式を解く 数学的準備No1 指数 数学的準備No2 対数 数学的準備No3 三角比,三角関数 数学的準備No4 三角関数の加法定理 数学的準備No5 ベクトル 数学的準備No6 数列 階差数列 数学的準備No7 微分・積分(1) 初等関数の微

確率統計キャンパス ゼミ 改訂6 Amazon Com Books
モーメント 意味 数学
モーメント 意味 数学-解決方法が見つかりました! HA David の論文「数学統計における共通用語の最初の(?)の出現」によれば、この状況での「モーメント」という言葉の最初の使用は、カールピアソンによる自然への13年の手紙「非対称周波数曲線」でした。 ネイマンの1938年のBiometrika論文「カールピアソンの モーメント (積率)母関数が役立つ理由 積率母関数という関数は一体どのような役に立つのでしょうか。 一部の例外を除いて『積率母関数さえ求めることが出来れば』 →それを微分して0を代入すると非常に簡単にモーメントが計算でき、 →さらに




力のモーメント の問題のわからないを5分で解決 映像授業のtry It トライイット
モーメント (数学)を解説文に含む見出し語の英和和英辞典の検索結果です。モーメント (数学)数学の確率論および関係した諸分野におけるモーメント (moment) または積率(せきりつ)とは、物理学におけるモーメントを抽象化した概念である。さて、偶力pは物体aを回転させます。つまり力のモーメントが作用するのです。偶力pによる力のモーメントは、 m=p×(l1 l2) となります。偶力の意味は、下記が参考になります。 偶力の基礎知識と、モーメントの関係 力のモーメントと曲げモーメントの違い応用数学 III:(5)大数の法則と中心極限定理 9 モーメント母関数の意味 •モーメント母関数はその名の通りモーメントを計算すると きにとっても便利です。 •試しに1回微分して見ましょう •ここでt=0ならば •おっとこれは平均ですね。 d!t dt = dE"#etX$% dt =E"#XetX$% d!t dt
数学の確率論および関係した諸分野におけるモーメント(moment)または積率(せきりつ)とは、物理学におけるモーメントを抽象化した概念である。 実変数xに関する関数mathf(x)\,/mathの mathn/math次モーメント math\mu^{(0)}_n/mathは、 数学 の 確率論 および関係した諸分野における モーメント (moment) または 積率 (せきりつ)とは、 物理学 における モーメント を抽象化した概念である。数学の確率論および関係した諸分野におけるモーメント(moment)または積率(せきりつ)とは、物理学におけるモーメントを抽象化した概念である。 実変数xに関する関数 f(x)\, の n 次モーメント \mu^_n は、 で表される。妥当な仮定の下で高次モーメントすべての情報から関数f(x)は一意に決定さ
大学理系専門予備校 Uni(ユニタス:https//unitasujp )のサンプル動画です。 確率統計学:ヨビノリたくみ 講師Uniは数学、モーメントの関数は、関数の形状に関連する定量的尺度であるグラフ。関数が質量を表す場合、最初のモーメントは質量の中心であり、2 番目のモーメントは回転慣性です。関数が確率分布の場合、最初のモーメントは期待値、2 番目の中心モーメントは分散、3 番目の標準化された数学のモーメントについては「モーメント (数学)」を、物理量のモーメントについては「モーメント」をご覧ください。 確率論 や 統計学 における モーメント ( 英 moment )または 積率 (せきりつ)とは、 確率変数 のべき乗に対する 期待値 で与えられる特性値。




Xrossval アクチュアリー数学 試験時間内に解き終えるために主要な確率分布に関しては 確率 密度 関数 平均 分散 モーメント母関数辺りは公式暗記しておいた方が良さそう感ある




徹底解説 モーメント 確率論 アクチュアリーでも頻出 確率論の重要概念をサクッと理解 徹底解説 統計学 松本ゆうや 数学 Kindleストア Amazon
偶モーメント 大きさが等しく、反対方向の2つの平行な力である 偶力によって生じるモーメント。 剛体に偶力だけが働く場合、剛体は並進運動を 伴わない回転運動だけを行う。 M = r1×Fr2×F = r×F A B O r1 r2 r F -F M モーメントNm r1,r2,r モーメントアームm F数学の確率論および関係した諸分野におけるモーメント (moment) または積率(せきりつ)とは、物理学におけるモーメントを抽象化した概念である。 実変数 x に関する関数 f(x) の n 次モーメント \({\displaystyle \mu _{n}^{(0)}}\) は、 \({\displaystyle \mu _{n}^{(0)}=\int _{数学、モーメントの 関数は、関数の形状に関連する定量的尺度である グラフ。 関数が質量を表す場合、最初のモーメントは質量の中心であり、2番目のモーメントは 回転慣性です。 関数が 確率分布の場合、最初のモーメントは 期待値、2番目の 中心モーメントは 分散、3番目の 標準化




モーメント 高校物理 力学 モーメント 力のモーメント 授業 Youtube




力のモーメント の問題のわからないを5分で解決 映像授業のtry It トライイット
法に比べ,モーメント法の物理的および数学的概念 は,工学系の学部生にとって掴みにくいように感じ ている.また計算コードを作成する際,プログラム上 のテクニックや数学的な予備知識も必要となモーメント (数学)がく 数学の確率論および関係した諸分野におけるモーメント()または積率(せきりつ)とは、物理学におけるモーメントを抽象化した概念である。 実変数''x''に関する関数 f(x)\, の n 次モーメント \mu^_n は、 で表される。妥当な仮定の下で高次モーメントすべての情報からJapanese dictionary search results for モーメント (数学) #sentence



慣性モーメント Zaudy S 日記




アクチュアリー数学合格体験記 数学 統計教室の和から株式会社
力のモーメントと偶力 (1) 知識・記憶レベル 難易度 ★ 右図のように剛体 の点 にそれぞれ力が働いている. 点 まわりのモーメントのつり合い式を答えよ. 点 まわりのモーメントのつり合い式を答え数学の確率論および関係した諸分野におけるモーメント( moment )または積率(せきりつ)とは、物理学におけるモーメントを抽象化した概念である。 実変数xに関する関数 の 次モーメント は、 モーメント母関数 M X (t) M_X(t) M X (t) を n n n 回微分して t = 0 t=0 t = 0 を代入すると E X n EX^n E X n となる。 モーメント母関数の重要な性質です。 導出には マクローリン展開 の知識が必要です。




幾何分布のモーメント母関数 特性関数とその導出証明 数学の景色




モーメント母関数の定義と使い方 モーメント母関数から期待値と分散を求めてみよう アタリマエ
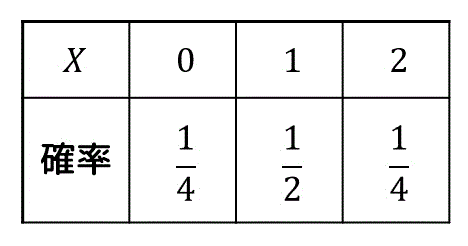
例えば、平均 E ( X) であれば、 E ( X) = ∑ i = 1 n x i p i = x 1 p 1 x 2 p 2 ⋯ x n p n で求めることができますね。 この x i の部分を ( x i − a) k としたものが k 次のモーメント となります。 式で表すと、 E ( ( X − a) k) = ∑ i = 1 n ( x i − a) k p i = ( x 1 − a) k p 1 ( x 2 − a) k p 2 ⋯ ( x n − a) k p n となります。 早速例題で2次のモーメントまで求めてみましょう。 例題1 力のモーメント 大学でも数学・物理を得意とし,情報系の学科に進みつつも,独学で勉強を続けている。 学びTimesでは主に「高校数学の美しい物語」「高校生から味わう理論物理入門」の記事執筆・修正業務に尽力している。Yz平面にある, x軸を回転軸とする車輪に, 位置r1=(0,1,0)に力F1=(0,0,2), 位置r2=(0,0,1)に力F2=(0,3,0)を加えた x軸の負の向きから見て車輪はどちらに回る




モーメント 確率論 Wikipedia



力のモーメントでなぜ 1 の腕の長さは0 5とするんでしょうか 0 8ではな Yahoo 知恵袋
例題:力のモーメントと偶力 (2) 数学活用大事典 ホーム 機械 工業力学(VA3 力学) 力のモーメントと偶力 力のモーメントと偶力 (2) 基礎知識 « 前の例題 力のモーメントと偶力 (1) 次の章 重心 確率分布におけるモーメントとモーメント母関数についてまとめます。 確率分布の形 確率分布の形を決める値として、期待値や分散があると思います。 例えば以下のような正規分布であれば、期待値 (平均) と分散がわかればその形を一意に決めることができます。 正規分布だけではない確モーメント (数学)せきりつ 数学の確率論および関係した諸分野におけるモーメント()または積率(せきりつ)とは、物理学におけるモーメントを抽象化した概念である。 実変数''x''に関する関数 f(x)\, の n 次モーメント \mu^_n は、 で表される。妥当な仮定の下で高次モーメントすべての情報



力のモーメントは外積で定義されている 高校物理 数学成績アップ術



2
したがって、求めたいモーメントの大きさはr ⊥ F=×sin30°×40=×1/2×40= 40Nm 。 さきほどと同じ解答になりましたね。 モーメントの向きにも注意!力のモーメントの問題を見る > すべての授業の「要点まとめノート」「問題・解答」をPDF無料ダウンロードできる 学校で使っている教科書にあわせて勉強できるFor the physical concept, see Moment (physics) In mathematics, the moments of a function are quantitative measures related to the shape of the function's graph If the function represents mass, then the first moment is the center of the mass, and the second moment is the rotational inertia




力のモーメント の問題のわからないを5分で解決 映像授業のtry It トライイット



物理の力のモーメントで出てくる 重心の求め方と数学に出てくる線分の内分点 Yahoo 知恵袋




確率統計キャンパス ゼミ 改訂6 Amazon Com Books




物理です 数学 Clear



数学ナビゲーター掲示板 One Thread Res View 確率の問題です 大至急お願い致します Page 0



うさぎでもわかるモーメント母関数 積率母関数 工業大学生ももやまのうさぎ塾




現代数学 1969年12月号 株式会社 現代数学社
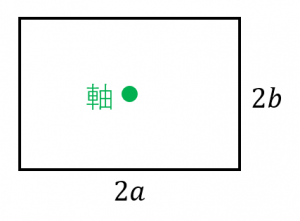



一様な長方形 正方形の慣性モーメントの2通りの計算 具体例で学ぶ数学




大学物理 剛体の力学入門 慣性モーメントの定義 全6回 力学 Youtube



2級建築施工管理技士の構造問題とモーメントの関係は 3分でわかる過去問の解き方と計算




二次モーメントに関する話 Qiita




著者モーメント パスカル




力のモーメントの公式 つりあいや単位も丸わかり 計算問題付き 高校生向け受験応援メディア 受験のミカタ
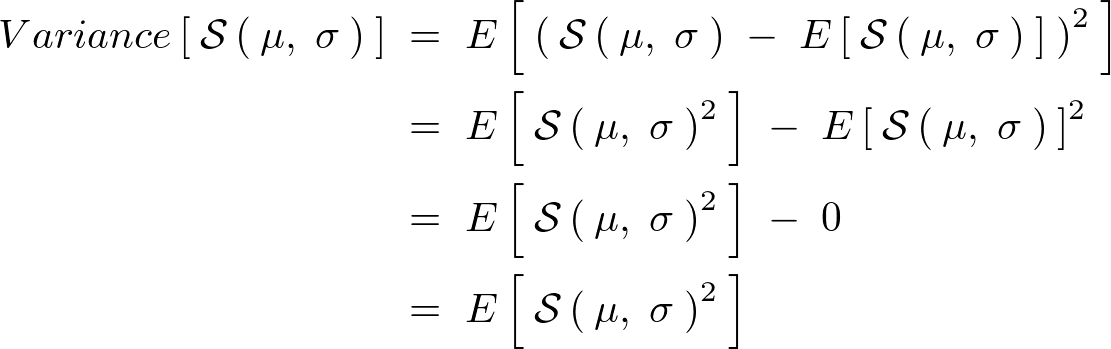



スコア関数の分散




モーメントの計算方法 2 Youtube



力のモーメントってなに 本当にわかるモーメントの意味と計算方法




力のモーメントの公式 つりあいや単位も丸わかり 計算問題付き 高校生向け受験応援メディア 受験のミカタ




偶力 高校物理 力学 モーメント 偶力のモーメント 授業 Youtube




すうがくぶんか على تويتر 10月開講講座 数理統計学では 統計検定1級レベルに必要な数理統計の知識について講義します 確率分布に関連した積分計算やモーメント 母関数 推定量の不偏性などの数学的性質などについて扱います オンライン開講で講義の録画を共有し




角運動量 Spin Angular Momentum について解説




Images Of モーメント 数学 Japaneseclass Jp




確率6 積率母関数の利用 Youtube




標準正規分布のモーメント母関数 標準正規分布のモーメント母関数を計 数学 教えて Goo
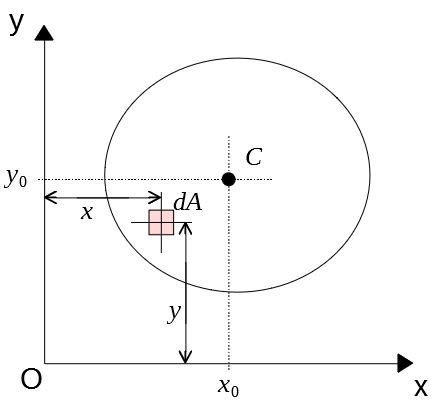



断面一次モーメント 面積モーメント と図心




積率 モーメント母関数の導出と意味 期待値や分散が求まる理由を解説




考え方を教えてください Clear



物理の力 剛体のつり合いが苦手です 力のモーメントが腕の長さ 力な Yahoo 知恵袋



重心 図形 幾何学 数学教育
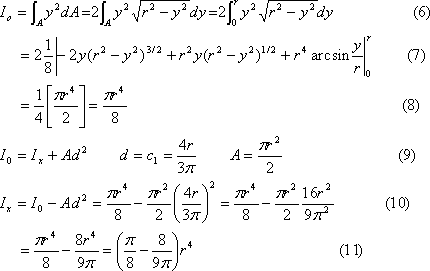



問題
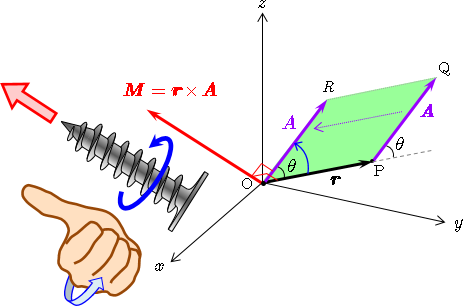



ベクトルのモーメント



例題 曲げ 6 数学活用大事典



慣性モーメントとは



1
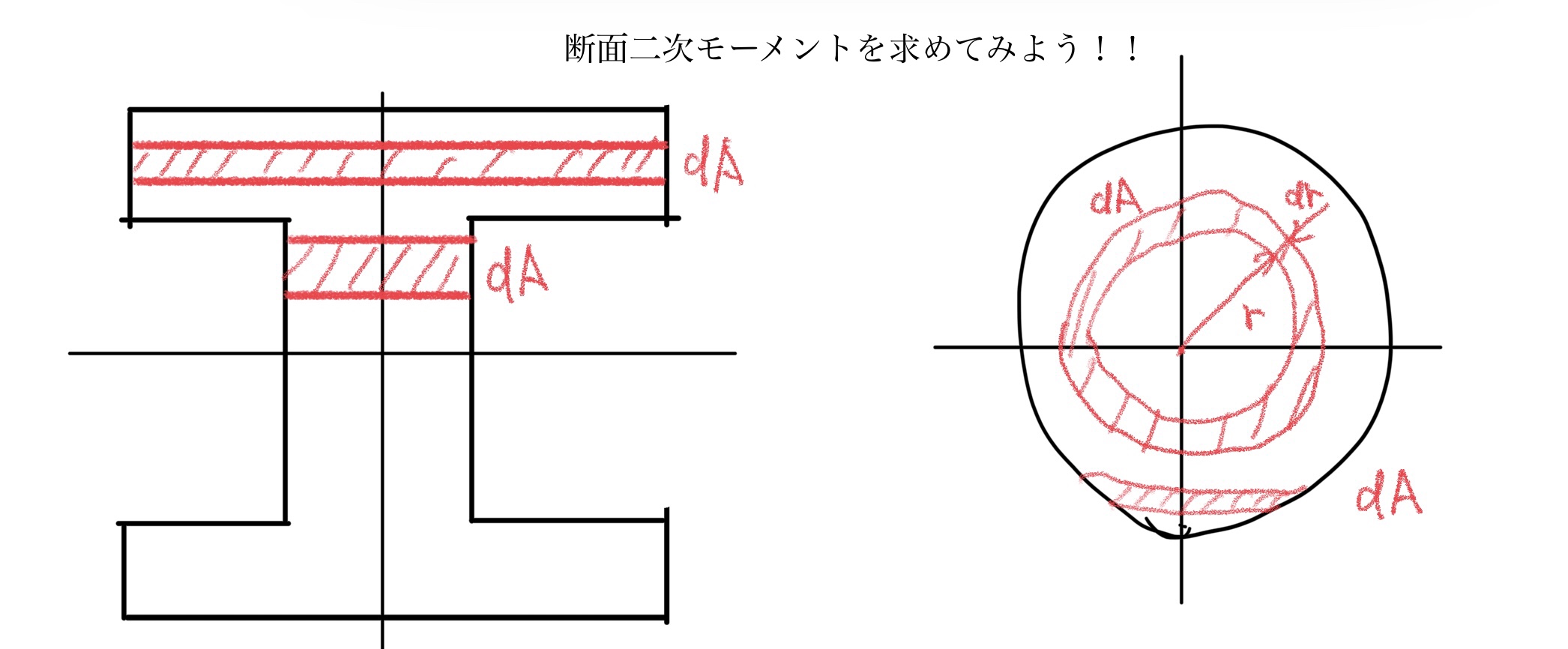



初心者でもわかる材料力学8 断面二次モーメントを求める 断面一次モーメント 断面二次モーメント




大学物理 剛体の力学入門 慣性モーメントの性質 全6回 力学 Youtube



例題 剛体の運動 2 数学活用大事典




すうがくぶんか على تويتر 10月開講講座 数理統計学では 統計検定1級レベルに必要な数理統計の知識について講義します 確率分布に関連した積分計算やモーメント 母関数 推定量の不偏性などの数学的性質などについて扱います オンライン開講で講義の録画を共有し




高校物理 力のモーメント Youtube




剛体のつり合い 力のモーメントの公式 解き方まとめ 理系ラボ




高校物理 力のモーメントの計算 映像授業のtry It トライイット



2




8th9bjfs0qfl M




5 2 モーメントとは People1993のブログ




高校物理 力学 剛体 力のモーメントの求め方 Youtube
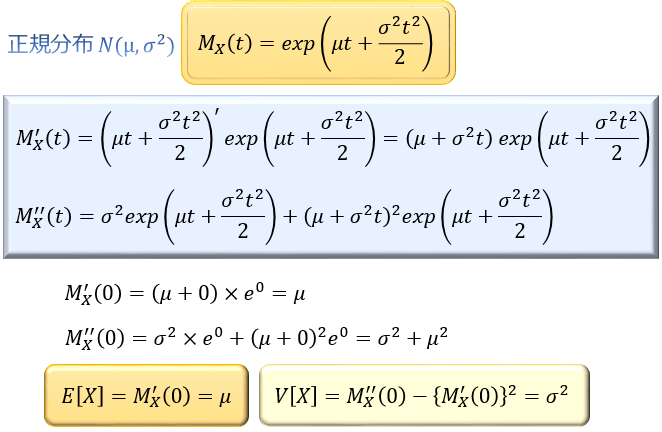



モーメント母関数の定義と使い方 モーメント母関数から期待値と分散を求めてみよう アタリマエ




モーメント 確率論 Wikipedia



剛体の運動 数学活用大事典




断面一次モーメント 面積モーメント と図心



うさぎでもわかるモーメント母関数 積率母関数 工業大学生ももやまのうさぎ塾




力のモーメント の問題のわからないを5分で解決 映像授業のtry It トライイット



初心者でもわかる材料力学8 断面二次モーメントを求める 断面一次モーメント 断面二次モーメント



Twitterモーメント一覧 随時更新 7931のあたまんなか



1




てこのつり合いの問題と解き方 支点を中心に左右のモーメントを計算する 小学理科 Irohabook



指数型分布族について Hello Cybernetics



力のモーメントと偶力 数学活用大事典




モーメント 数学 Moment Mathematics Japaneseclass Jp




力のモーメント演習6 Physicmath フィジクマス



モーメント母関数についての質問です 数学のバックグラウンドは数 Yahoo 知恵袋




21重要な曲げモーメント図に関連する質問と回答




モーメント母関数の意味と具体例 高校数学の美しい物語



1




資料 Manavee Manualzz




モーメント 数学 Moment Mathematics Japaneseclass Jp



力のモーメントってなに 本当にわかるモーメントの意味と計算方法




力のモーメント の勉強法のわからないを5分で解決 映像授業のtry It トライイット



質問です 標準正規分布のモーメント母関数を計算した 3次モーメントと4次モー Yahoo 知恵袋
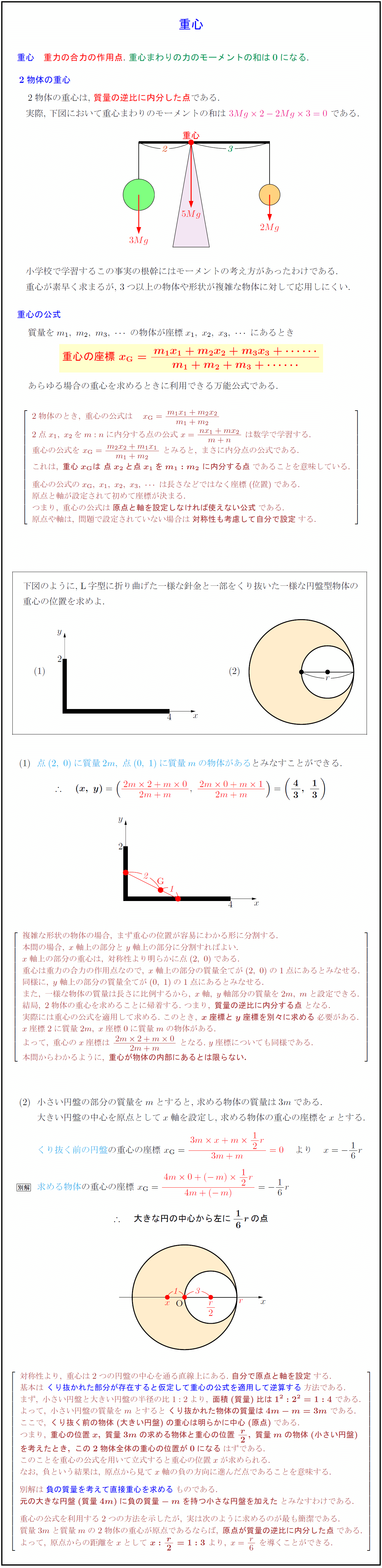



高校物理 剛体の力学 重心 L字型物体 一部がくり抜かれた物体 重心の公式 受験の月



力のモーメントと偶力 数学活用大事典




Images Of モーメント 数学 Japaneseclass Jp



ねじれ角の問題です 断面2次極モーメントを求め 積分するときに 解答では Yahoo 知恵袋




モーメント 確率論 Wikipedia
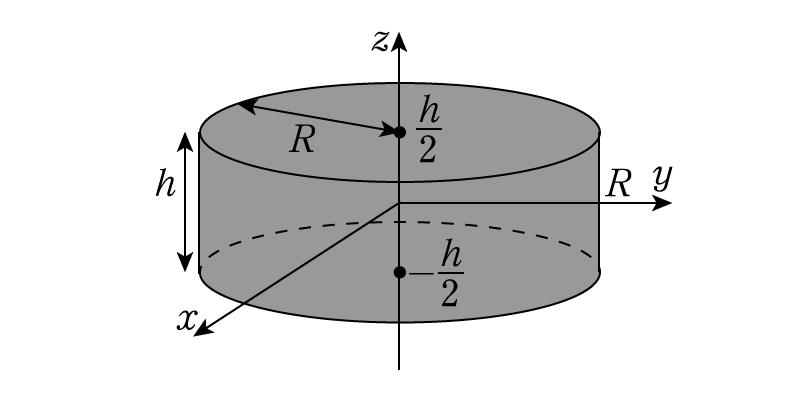



剛体の慣性モーメントの計算 物理の学校




円筒側面を転がる円板が側面を離れる位置 特殊相対性理論 電磁気学 数学




高校物理 剛体のつりあい 映像授業のtry It トライイット




電気磁気工学を学ぶ 球の慣性モーメント



1




ろき Moment Ringと打とうとして検索候補にびっくりしたんだけど 確率論の分布平均や数学の積率なんかを モーメント と呼ぶそうで 計算式を書く時にこれを表す記号が M なのね ちょっと畑せんせーこれも狙ったのー T Co




剛体のつり合い 力のモーメントの公式 解き方まとめ 理系ラボ




母数と統計量




モーメント母関数の意味と具体例 高校数学の美しい物語



確率統計の復習 離散型確率分布のモーメント母関数 かくれが




モーメント 数学 Moment Mathematics Japaneseclass Jp




L モーメント法の手順をまとめました モーメント 近似 連立の3段階構成です 数学 統計検定




数学の景色 さまざまな数学を概観
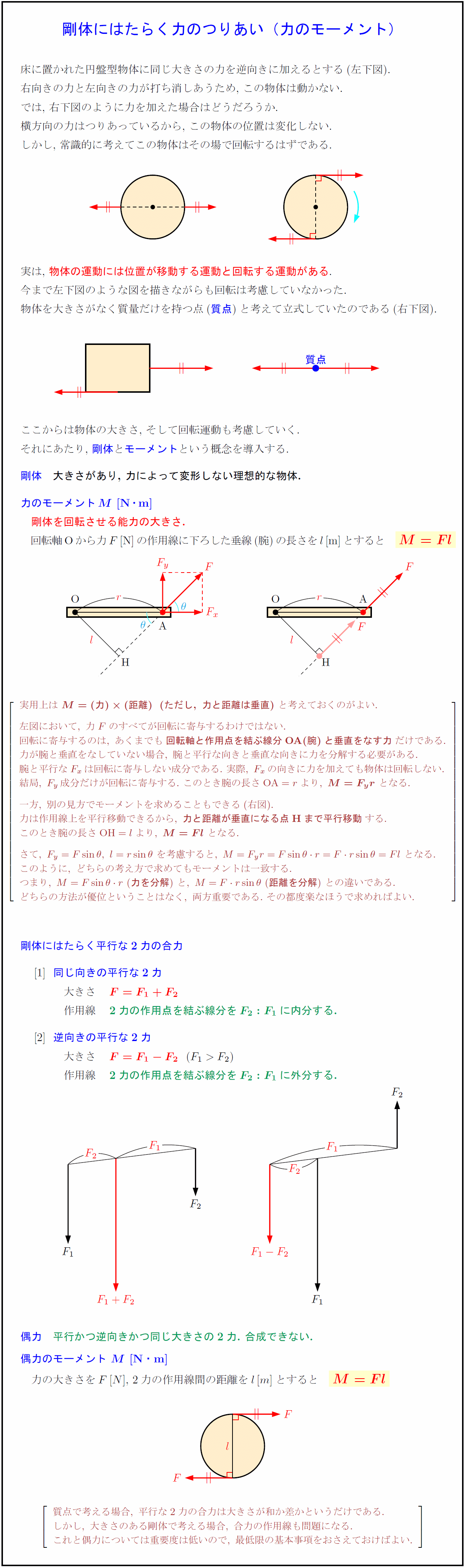



高校物理 剛体にはたらく力のつりあい 力のモーメント 受験の月




例題解説 外積で力のモーメントを計算しよう 物理数学 演習i 05 L04 Youtube




数学 物理学 数式 Pixabayの無料写真




モーメント 数学 Moment Mathematics Japaneseclass Jp



物理のモーメントの和の基本問題なのですが 点aの周りのモーメントの Yahoo 知恵袋




最終講義 武蔵工業大学 数学部門 有本彰雄 Ppt Download




モーメント 確率論 Wikipedia


コメント
コメントを投稿